Bounding box of cubic bezier curve
Bounding box of cubic bezier curve
Created: 21 September 2016 Last updated: 7.04.2018
Background
It is very commonly used approach to itterate through the points of the bezier
curve and this way to determine the most left, right, top, bottom possitions.
This approach is slow and not so accurate.
Basics
Line segment equations
P = A + (B - A)t where t changes from 0 to 1.
P = A + Bt - At
P = (1-t)A + tB
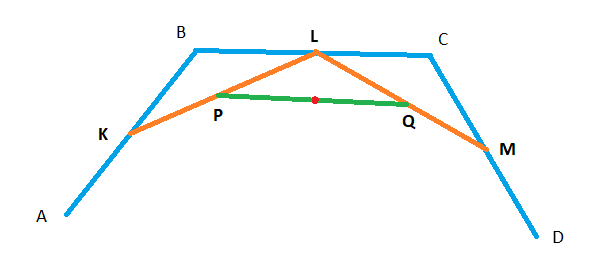
Bounding box border
The bounding box border can be formed by the end points of the cubic bezier curve or by inner point.
The inner point should have a vertical slope for left and right border and horizontal slope for top bottom borders.
Calculations
To have vertical or horizontal slope P and Q should be equal
P = Q
P = K + (L - K)t
Q = L + (M - L)t
Substitute in P = Q
K + (L - K)t = L + (M - L)t
K - L + (L - K)t - (M - L)t = 0
K - L + (L - K - M + L)t = 0
(2L - K - M)t + (K - L) = 0
We have for K, L, M
K = A + (B - A)t
L = B + (C - B)t
M = C + (D - C)t
Substitute in (2L - K - M)t + (K - L) = 0
(2*(B + (C - B)t) - (A + (B - A)t) - (C + (D - C)t))t + (A + (B - A)t) - (B + (C - B)t) = 0
(2*(B + Ct - Bt) - (A + Bt - At) - (C + Dt - Ct))t + (A + Bt - At) - (B + Ct - Bt) = 0
(2*B + 2*Ct - 2*Bt - A - Bt + At - C - Dt + Ct)t + A + Bt - At - B - Ct + Bt = 0
(2*Ct - 2*Bt - Bt + At - Dt + Ct + 2*B - C - A)t + A + Bt - At - B - Ct + Bt = 0
(3*Ct - 3*Bt + At - Dt + 2*B - C - A)t + A + Bt - At - B - Ct + Bt = 0
(3*C - 3*B + A - D)tt + (2*B - C - A)2t + A - B = 0
a = 3(C - B) + A - D
b = 2(2*B - C - A)
c = A - B
To find the value we have to solve Quadratic quation
at^2 + bt + c = 0